Energy Eigenvalues and Eigenfunctions of a Diatomic Molecule in Quadratic Exponential-type Potential

Abstract

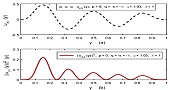
We have employed the exact quantization rule to obtain closed form expression for the bound state energy eigenvalues of a molecule in quadratic exponential-type potential. To deal with the spin-orbit centrifugal term of the effective potential energy function, we have used a Pekeris-type approximation scheme, we have also obtained closed form expression for the normalized radial wave functions by solving the Riccati equation with quadratic exponential-type potential. Using our derived energy eigenvalue formula, we have deduced expressions for the bound state energy eigenvalues of the Hulthén, Eckart and Deng-Fan potentials, considered as special cases of the quadratic exponential-type potential. Our deduced energy eigenvalues are in excellent agreement with those in the literature. We have computed bound states energy eigenvalues for six diatomic molecules viz: HCl, LiH, H₂, SeH, VH and TiH. Our results are in total agreement with existing results in the literature for the s-wave and in good agreement for higher quantum states. By solving the Riccati equation, we have obtained normalized radial wave functions of the quadratic exponential-type potential, our results show higher probabilities of finding the molecule in the region 0.1 ≤ y ≤ 0.2