Application of the Schwarz-Christoffel Transformation to the Solution of Harmonic Dirichlet Problems in Electrostatics
DOI:
Keywords:
Conformal Map, Schwarz-Christoffel Map, Analytic Function, Branch of a Multiple Valued Function, Electrostatic Potential, Electric field IntensityAbstract
In this paper, a purely conformal mapping method for efficiently solving harmonic Dirichlet problems of electrostatic in domains free of charge and with charge whose boundaries have inconvenient geometries consisting of straight-line segments is presented. The method which uses the inverse of an appropriately determined Schwarz-Christoffel transformation as the mapping function, was applied to harmonic Dirichlet problems in an infinite strip and infinite sector and the solution or electrostatic potential for the problem obtained for each case. Furthermore, the equipotential lines of the electric field were also obtained in order to show the features of the solution and the field analysed accordingly. The electric field intensity was also analysed to show its variation in the field. This method could therefore be a suitable alternative method for solving Laplace's equation in two dimensional electrostatic problems.
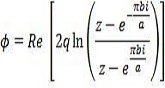


 Contact Us
Contact Us Editorial Team
Editorial Team Join As A Reviewer
Join As A Reviewer  Request For Print Copy
Request For Print Copy


 Cprint Publishers
Cprint Publishers