The Minimum Spanning Tree of the Nigeria Roads Network through Multiple-Roads Network System

Abstract

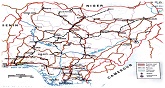
The research work is aimed at finding the optimal graph of the Travel Salesman Problem of the vehicular movement from multiple sources of the Nigeria roads network of the coastal towns: Lagos, Port Harcourt, Asaba and Calabar through the hinterland to multiple destinations (border towns) of Katsina, Sokoto and Maiduguri so as to minimize the cost of fueling, maintenance and loss customers and goods/services get delivered to destinations in good time. In obtaining the optimal graph, the Kruskal algorithm of the minimum spinning tree was used and was implemented by a computer application package, TORA, developed by Taha. The optimal minimum spinning graph is: Lagos – Abeokuta – Ibadan – Osogbo – Ilorin – Osogbo – Akure - Ado Ekiti – Akure – Benni – Asaba – Owerri - Port Harcourt – Umuahia – Uyo – Calabar – Uyo – Umuahia - Port Harcourt – Owerri – Asaba – Benni – Awka – Enugu – Abakelike – Enugu – Awka – Benni – Akure – Lokoja – Abuja – Minna –Abuja – Kaduna – Kano – Katsina - Kano – Dutse – Kano – Gasua – Sokoto – Brini Kebbi – Sokoto – Gusau – Kano – Kaduna - Abuja – Lafia – Makurdi – Lafia – Jos – Bauchi – Gombe – Yola – Jalingo – Yola – Gombe – Damaturu – Maiduguri with the total distance of 8327Km.